×



Construcții geometrice Sisteme de proiecție Epura punctului Epura dreptei Epura planului Poliedre Curbe tehnice Cilindro-conice Sfera Suprafețe de rotație Suprafețe riglate Suprafețe elicoidale


Pagina de început Geometrie descriptivă Desen tehnic
Grafică Planuri calendaristice Utile

Curbe tehnice

☰ Deschide

Ovoidul

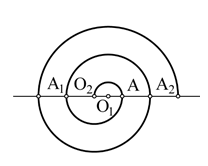
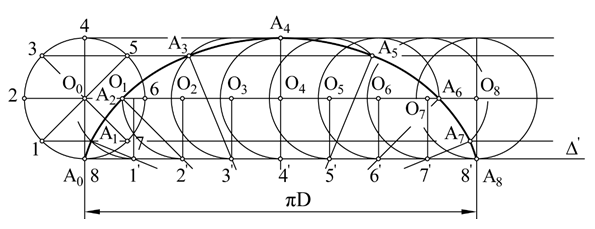
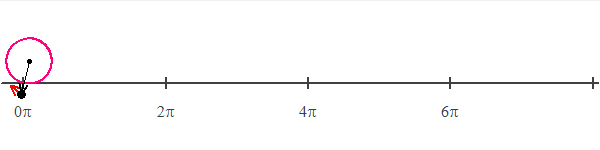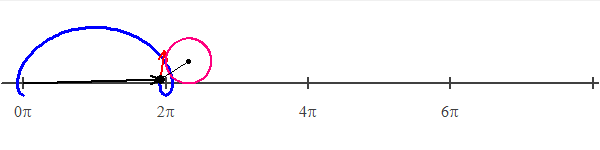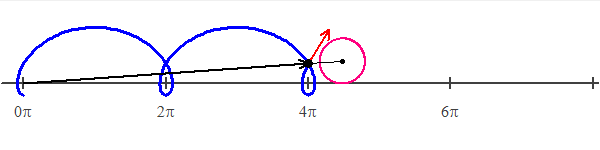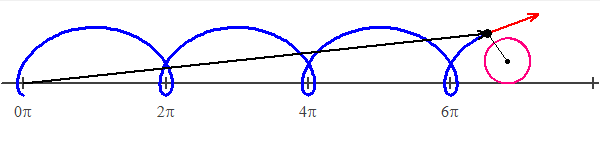
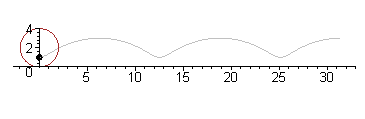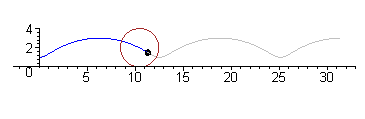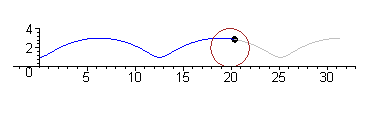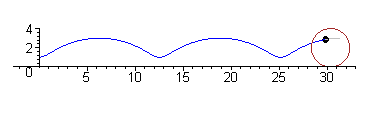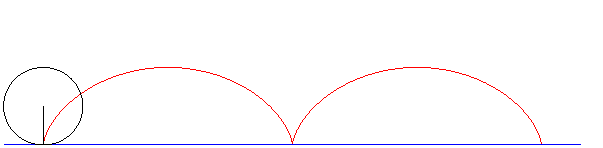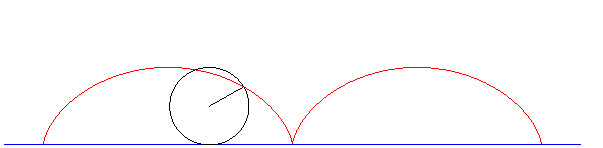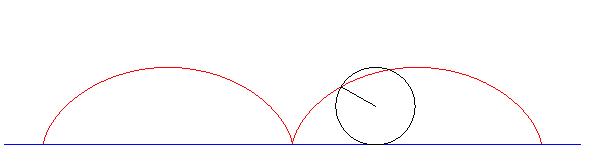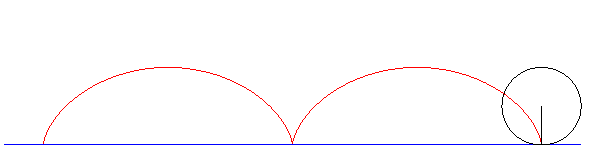
           Ovoidul este o curbă plană închisă formată din arce de cerc racordate şi simetrice faţă de o axă. Fiind dată axa mică AB, ovoidul se construieşte cu compasul luând o rază R, egală cu jumătate din axa mică şi trasând cercul cu centrul în O, OA = OB. Se trasează axa OC perpendiculară pe AB şi dreptele AC şi BC. Din punctele A şi B ca centre, cu raza AB, se trasează arcele BE şi AD. Apoi, din punctul C ca centru, cu raza CD sau CE, se trasează arcul DE, care se racordează în punctele D şi E.

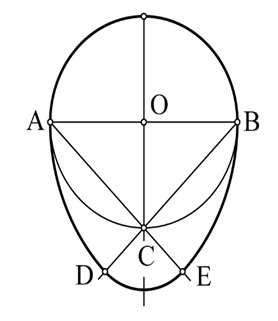
Ovoidul

Spirala

           Se consideră spirala cu două centre, cu pasul dat, formată din arce de cerc, din figura alăturată. Pentru trasarea ei, pe o dreaptă se ia segmentul O1O2, egal cu jumătate din pasul spiralei (pasul este distanţa dintre două spire consecutive). Din punctul O1, ca centru, raza O1O2, se trasează semicercul O2A. Apoi din punctul O2, ca centru, se trasează semicercul AA1. Se schimbă centrul în punctul O1, trasându-se semicercul A1A2 cu raza O1A1. Această operație se continuă până se obține spirala cu numărul de spire cerut.

Spirala

Elipsa

           În figura alăturată elipsa este reprezentată prin metoda cercurilor concentrice, metodă suficient de precisă pentru lucrările legate de reprezentări grafice. Fiind date lungimile celor două axe ale elipsei AB şi CD, din centrul O se trasează două cercuri concentrice, unul având ca diametru axa mică, iar cel de al doilea, axa mare. Se împart cele două cercuri în acelaşi număr de părţi (douăsprezece în cazul figurii alăturate), iar prin punctele de pe cercul mic se trasează paralele la axa mare şi prin punctele de pe cercul mare se trasează paralele la axa mică. La intersecţia acestora se determină puncte ale elipsei. Conturul elipsei se trasează unind punctele determinate, cu florarul.

Elipsa

Parabola

           Pentru construirea parabolei există diverse metode, dintre care în figura alăturată se indică metoda clasică (prin puncte). Pentru construirea parabolei după această metodă se dau focarul F şi directoarea parabolei. Prin punctul F, se duce axa parabolei BA, perpendiculară pe directoarea DD’, iar la jumătatea segmentului FB se fixează vârful A al parabolei. Se iau pe axa BA câteva puncte arbitrare (1÷4) prin care se duc tot atâtea pa¬ralele la directoare. Cu centrul în F şi cu o rază egală cu lungimea segmentului 1B, se intersectează dreapta dusă prin 1, în punctele M1 şi M’1, care aparţin parabolei. Apoi, din acelaşi centru, dar cu raza 2B se determină alte două puncte M2 şi M’2 pe dreapta dusă prin 2. În acelaşi mod se determină și celelalte puncte care se unesc printr-o curbă continuă cu ajutorul florarului.

Parabola

Hiperbola

           Trasarea hiperbolei se poate face în mai multe moduri, în figura alaturată exemplificându-se metoda trasării prin puncte, dându-se focarele F1 și F2 şi diferenţa razelor vectoare AB. Pe axa focarelor se marchează poziţia focarului precum şi câteva puncte arbitrare 1, 2, 3, 4 etc. Cu centrul în F2, luând ca rază segmentul A-1, se trasează un arc de cerc de o parte şi de alta a axei focarelor, care se intersectează cu un al doilea arc de cerc cu raza egală cu segmentul B-1 şi având ca centru focarul F1. Punctele astfel obţinute aparţin hiperbolei. Ramura din stânga se obţine, modificând ordinea razelor cu care se trasează arcele de cerc din cele două focare. Asimptotele hiperbolei sunt două drepte concurente în centrul O al hiperbolei şi tangente în punctele de la infinit ale curbei. Tangentele la hiperbolă în vârfurile A şi B ale curbei sunt paralele cu axa verticală. Dacă prin punctele de intersecţie cu asimptotele celor două tangente duse prin A şi B se duc paralele la axa orizontală, se obţine un dreptunghi (CEGD), care are drept laturi lungimile axelor hiperbolei şi diagonalele după asimptotele acesteia. Hiperbola pentru care dreptunghiul axelor devine un pătrat, se numeşte hiperbolă echilaterală.

Hiperbola

Cicloida

           În figura alăturată este prezentată trasarea grafică a cicloidei normale. Cercul generator este tangent dreptei directoare Δ. Se împarte cercul într-un număr de părţi (8 în exemplul dat), care se transpun pe dreapta directoare (81 = 81’, 12 = 1’2’...). Deoarece cercul generator se rostogoleşte pe dreapta directoare, se reprezintă cercul consecutiv cu centrul în punctele O1, O2, ...O8 şi se intersectează cu dreptele trasate prin punctele de divizare ale cercului generator, paralele cu drepta directoare Δ, obţinându-se astfel punctele cicloidei A0, A1, A2 ..., A8.
Cicloida normală
Cicloida normală -animaţie-
Cicloidă scurtată -animaţie-
Cicloidă alungită -animaţie-

Evolventa

           Evolventa sau desfăşurata cercului este o curbă plană care este generată de un punct al unei drepte generatoare, prin rostogolirea ei fără alunecare pe un cerc fix, numit cerc de bază. La construcția grafică a evolventei, se pot trasa două ramuri simetrice ale acesteia. În figura alăturată, pentru construcţia ramurii stângi, se trasează cercul director cu centrul în O, se împarte cercul într-un număr de părţi egale (12 părţi) şi în punctele de diviziune se trasează tangentele aferente acestor puncte.

Evolventa

Elicea cilindrică


           Elicea cilindrică reprezintă o curbă spaţială descrisă de un punct care se translatează uniform de-a lungul generatoarei unui cilindru circular drept, care în acelaşi timp, se roteşte uniform în jurul axei proprii. În timpul unei rotaţii complete a cilindrului, punctul descrie o curbă, numită spiră. Distanţa parcursă de punct de-a lungul unei generatoare, în timpul unei rotaţii, reprezintă pasul elicei. Construcţia grafică a elicei s-a făcut împărţind pasul p şi cercul de bază într-un număr n (n = 12) de părţi egale.
Elicea cilindrică

           Construcţia grafică a unei elice conice, pornind de la conul din figura de mai jos, se face în mod analog elicei cilindrice. Pentru obţinerea proiecţiei verticale a elicei conice se unesc punctele de intersecţie dintre paralelele duse la baza conului prin diviziunile pasului, cu generatoarele conului duse prin diviziunile bazei rezultând o sinusoidă. Proiecţia orizontală a elicei conice este o curbă de forma spiralei lui Arhimede, obţinută prin unirea punctelor de intersecţie dintre generatoarele conului duse prin diviziunile bazei, cu arcele de cerc cu centrul în centrul bazei, duse prin diviziunile proiecţiei pasului elicei pe planul orizontal.
Elicea conică


© GDGI