Drepte și unghiuri
|
|
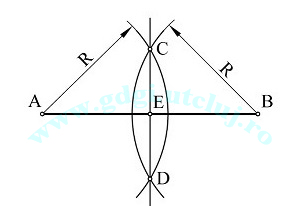 Împărțirea unui segment de dreaptă în două părți egale Împărțirea unui segment de dreaptă în două părți egale |
|
|
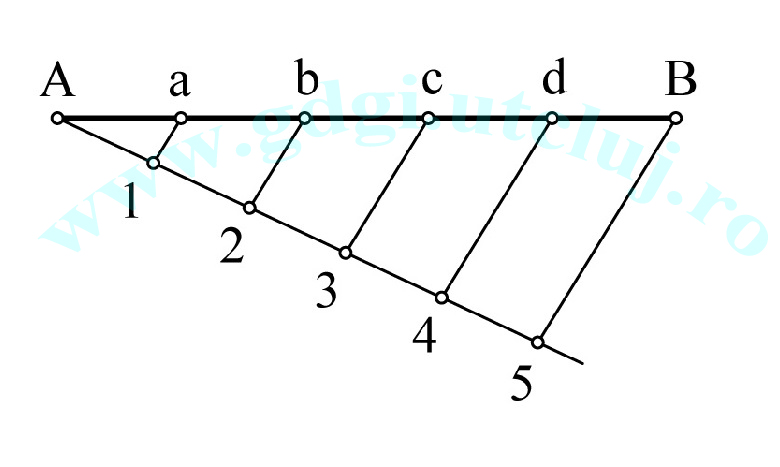 Împărțirea unui segment de dreaptă în "n" părți egale Împărțirea unui segment de dreaptă în "n" părți egale |
|
|
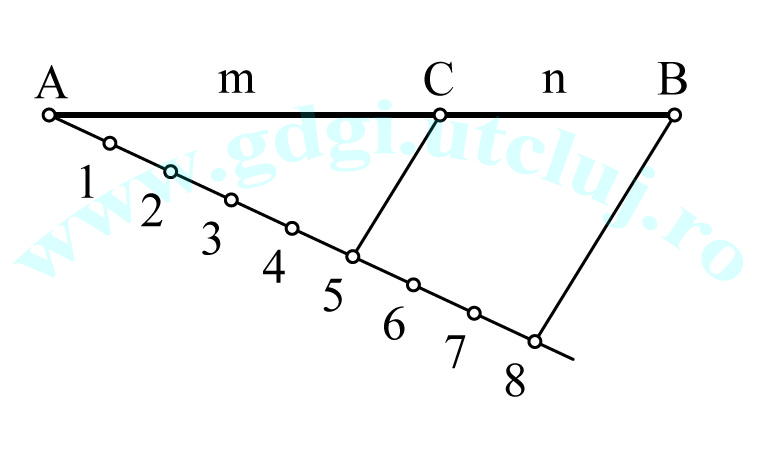 Împărțirea unui segment de dreaptă într-un raport dat Împărțirea unui segment de dreaptă într-un raport dat |
Racordări
|
|
 |
| Împărțirea unui segment de dreaptă într-un raport dat |
|
|
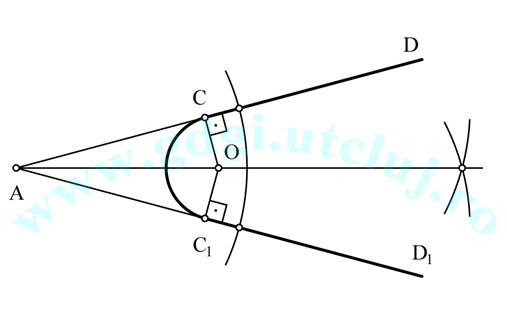
Racordarea a două drepte concurente
|
|
|
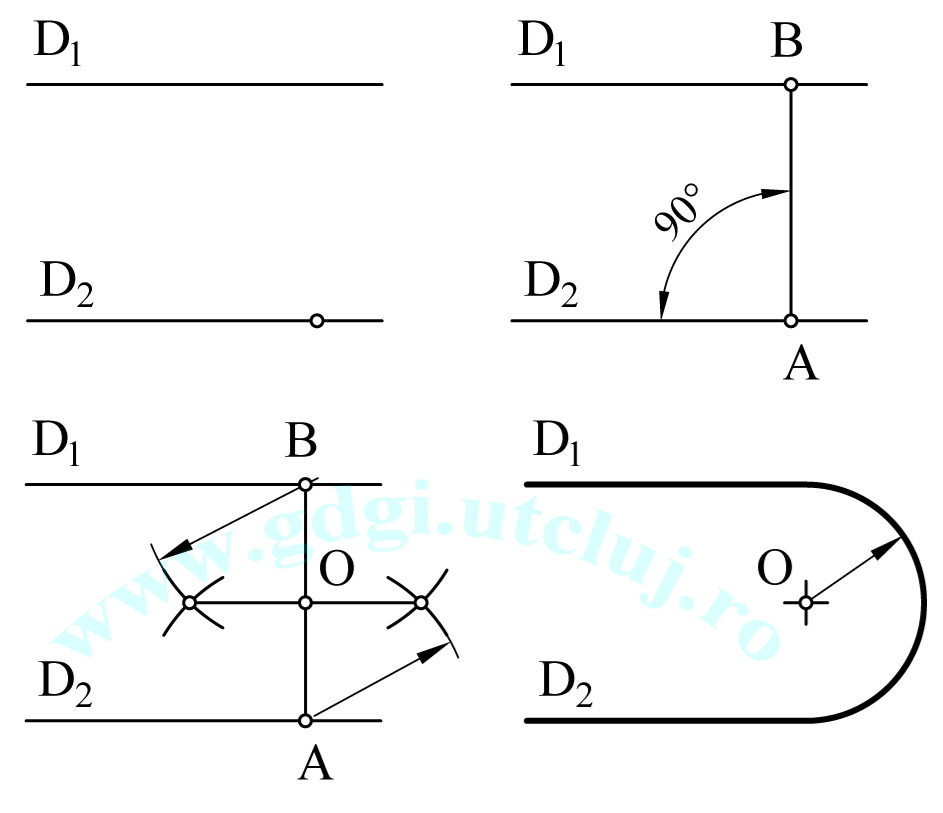
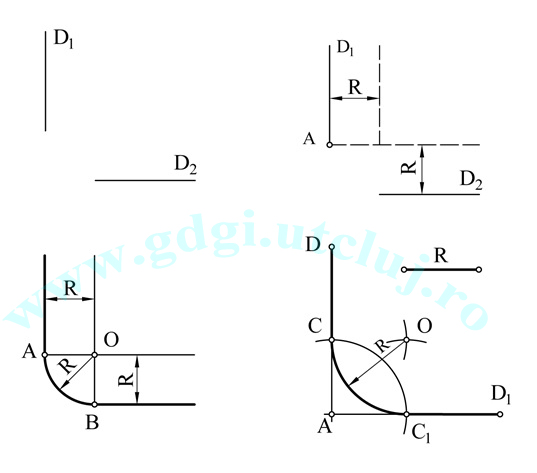 Racordarea a două drepte perpendiculare Racordarea a două drepte perpendiculare |
|
|
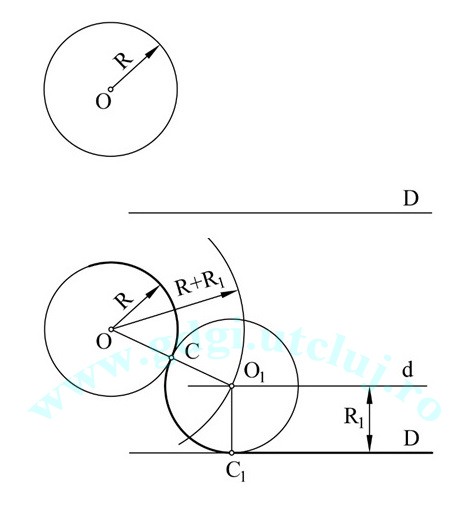 Racordarea unei drepte cu un cerc Racordarea unei drepte cu un cerc |
|
|
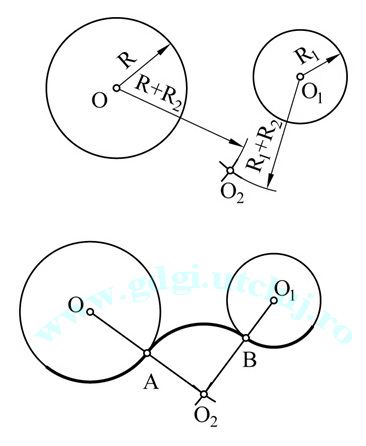 Racordarea exterioară a două cercuri Racordarea exterioară a două cercuri |
|
|
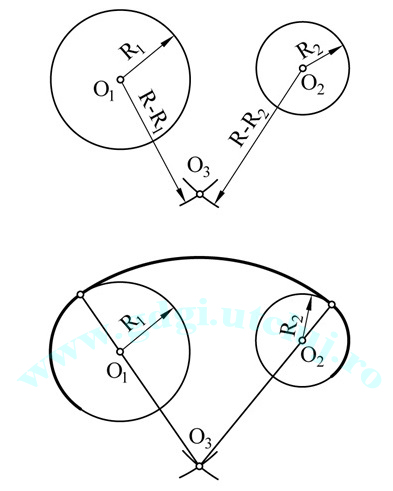 Racordarea interioară a două cercuri Racordarea interioară a două cercuri |
Poligoane regulate
|
|
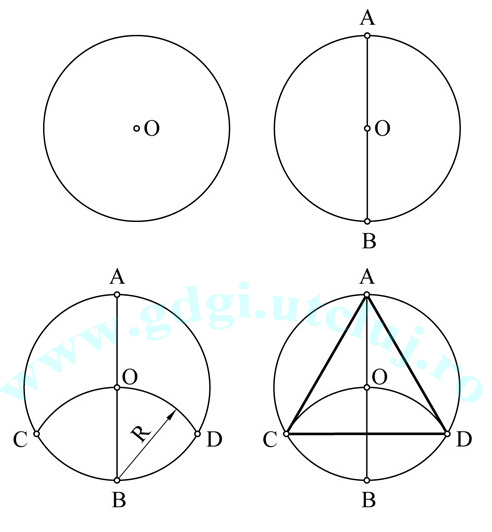 Construcția triunghiului echilateral Construcția triunghiului echilateral |
|
|
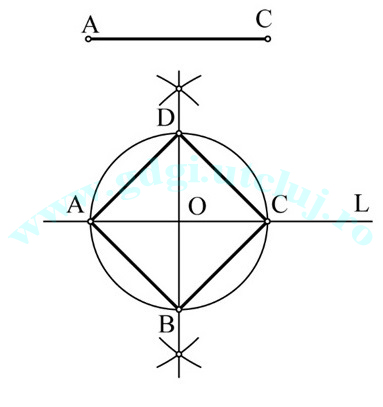 Construcția pătratului Construcția pătratului |
|
|
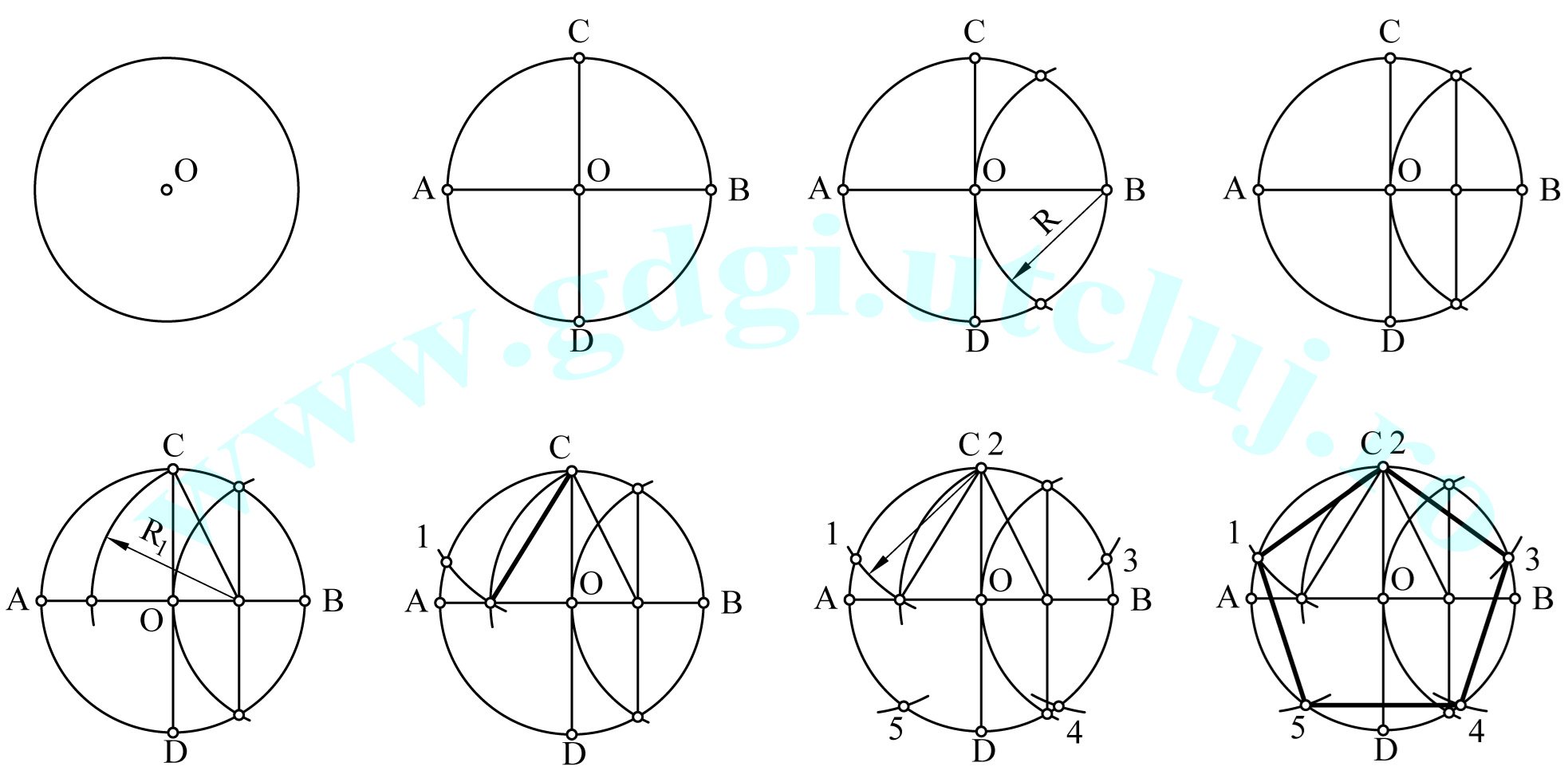 Construcția pentagonului Construcția pentagonului |
|
|
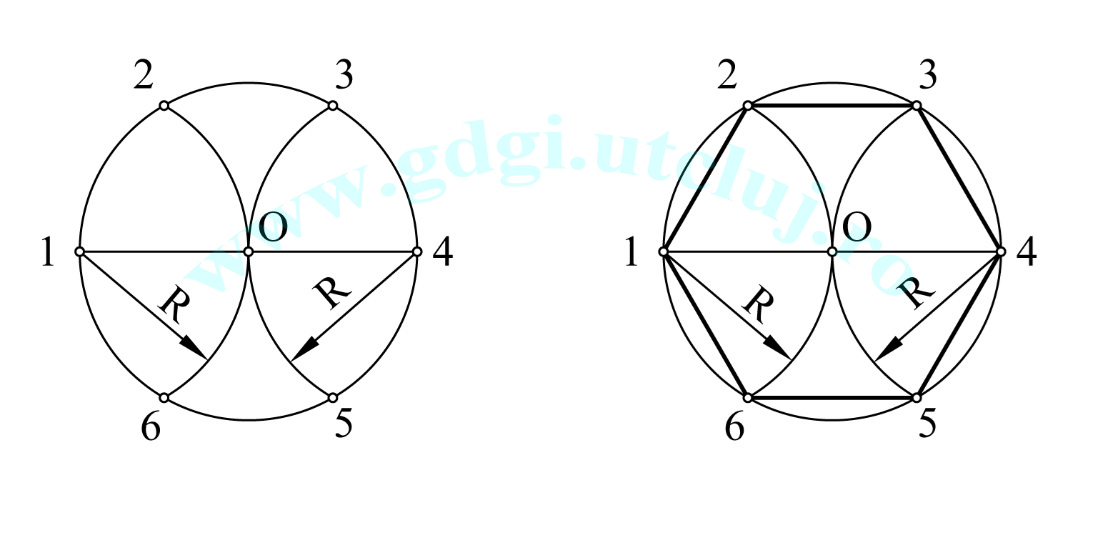 Construcția hexagonului Construcția hexagonului |
|
|
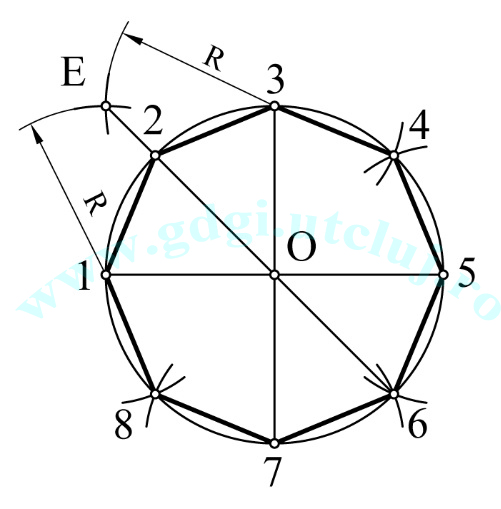 Construcția octogonului Construcția octogonului |
|
|
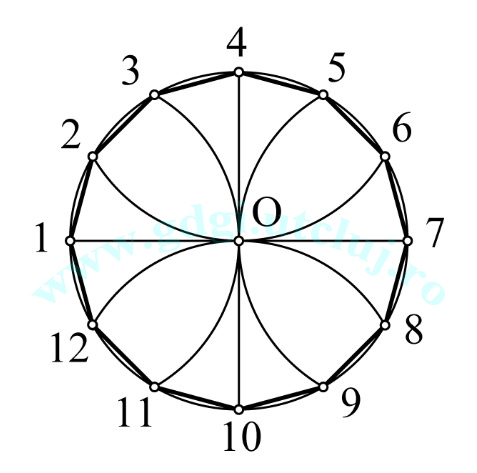 Construcția dodecagonului Construcția dodecagonului |